In this series of posts, we will give you an overview of the popular myths and help you understand what is going on in your Finite-Volume CFD code and how to interpret mesh quality checks for your problem. The goal of this post is to de-mystify the impact of various common cell types on accuracy in CFD meshing.
In the previous posts about Skewness and Non-orthogonality, it has often been said that the discretisation error is a sum of approximation errors at the faces of the cell. The goal of this post is to discuss how the cell type influences discretisation error and provide experimental evidence of how the theory applies in practice.
4 common cell types
The analysis is provided for four common cell types:
- Quadrilateral
- Triangle
- Hexagon
- Split-quad – it is a pentagon, but in the CFD jargon, it represents a quad cell whose neighbour has been refined.
To simplify the analysis, cells will be of ideal shape to avoid the influence of skewness, non-orthogonality, etc., and to get an idea of how ideal shapes perform against each other.
Convection term
In the first and the second post of this series, we discussed the Finite Volume discretisation of the Convection term, where the integral over the volume is transformed into the integral over the surface area. It was also shown that the discretisation practice is a sum of fluxes through the faces of the control volume. The goal here is to show how this influences the error.
The analysis for the convection term is performed by using a linear (Central Differencing) and a constant transport velocity. This scheme is a natural second-order interpolation scheme, and it is used to show the differences in expected accuracy in the ideal case.
Quadrilateral
A stencil of a 2D mesh consisting of squares is available below:
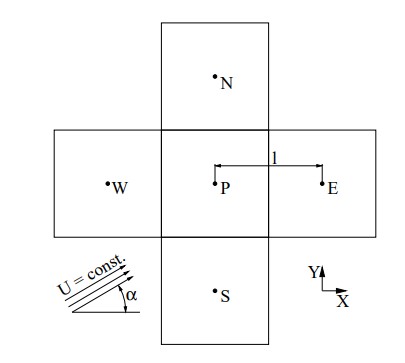
The mesh is both uniform and not skewed. By summing the error contribution over the four faces, the result is:
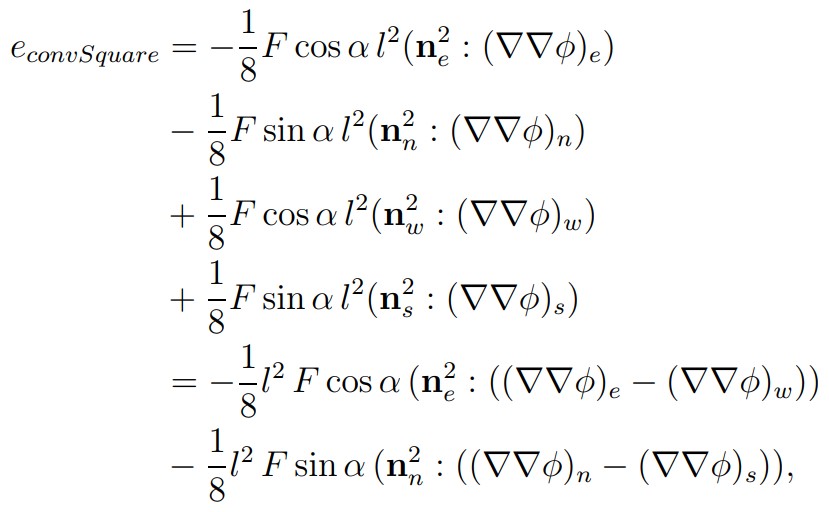
And it shows the following:
- Errors committed on opposite faces cancel themselves out.
- When the mesh is aligned with the flow, a flux through most faces can be zero, and this further reduces the error.
Triangle
A stencil consisting of triangles has the form:
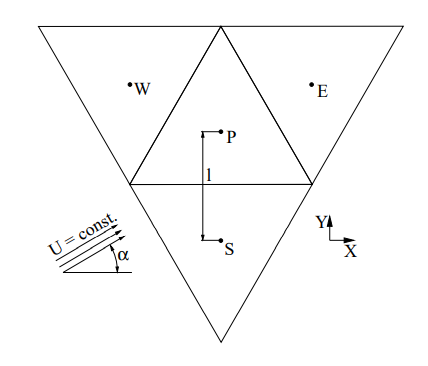
This mesh is both uniform and not skewed. Summing the error contributions over the faces results in:
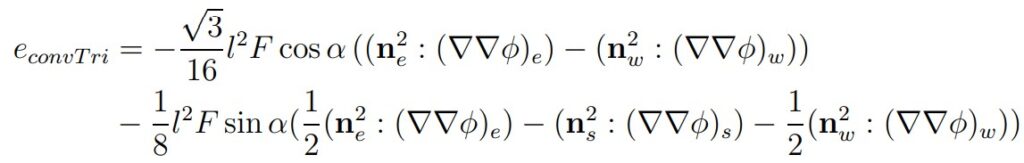
Shows that:
- The effect of error cancellation is far less pronounced because the face pairs do not exist.
- When the mesh is aligned with the flow, a flux through most faces can be zero, and this further reduces the error.
Hexagon
A mesh consisting of hexagons is uniform and not skewed. A stencil consisting of hexagons has the form:
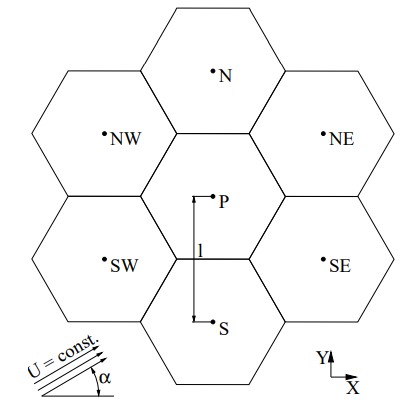
The summations of errors over faces show the following:
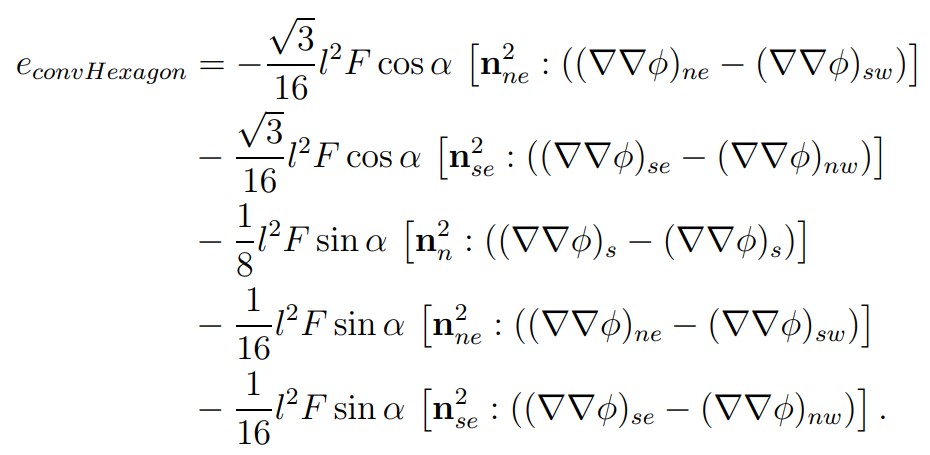
The equation above shows that:
- Error cancellation is present due to face pairs.
- When the mesh is aligned with the flow, a flux through most faces can be zero, and this further reduces the error. Not as much as for a square mesh, because there always exist more than two faces contributing to the error.
Split-quad
Split-hexes can appear in various forms, and are common in automatic mesh generation packages, appearing at transition regions between fine and coarse cells. A mesh consisting of split-squares is uniform and skewed. A stencil has the form:
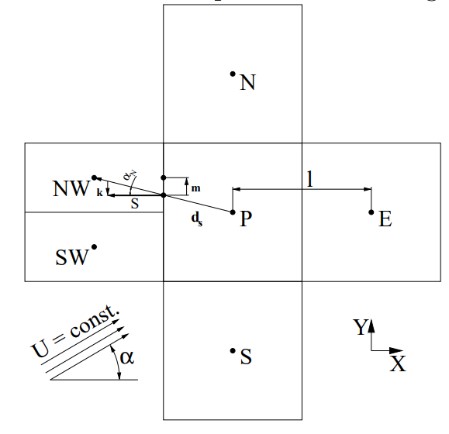
The summation of errors over faces shows the following:
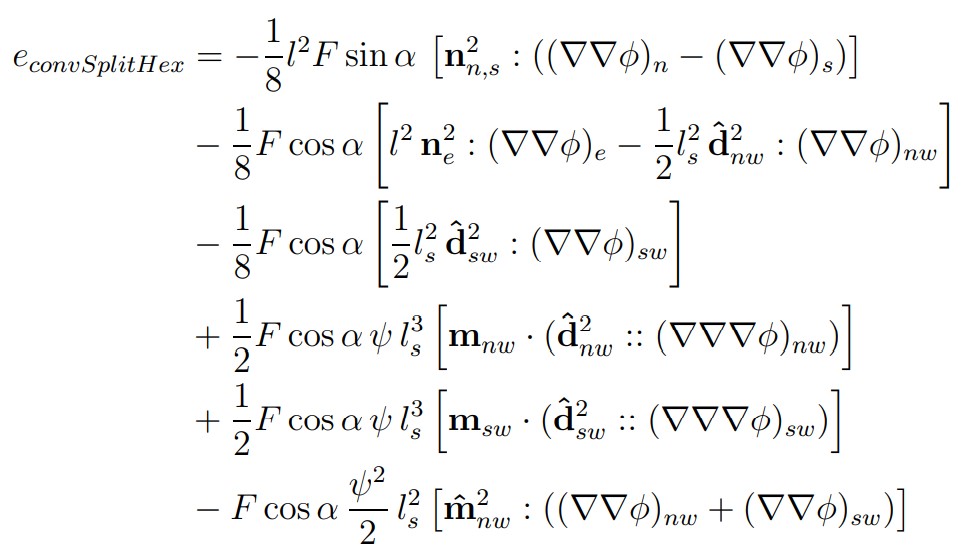
The conclusions that can be drawn are:
- Error cancellation due to face pairs is not pronounced anymore. Hence, this cell type is expected to result in a larger error compared to quad cells.
- Skewness cannot be avoided and it also increases discretisation error.
- When the mesh is aligned with the flow, a flux through most faces can be zero, and this further reduces the error. Not as much as for a square mesh.
Comparison depending on the solution type
From the expression given above it is noticeable that the error depends on the mesh, represented by n, I, and d, and the solution itself, represented by the gradients of the solution. Let us now analyse what happens for various types of solutions:
- ∇ϕ=const. – no error on any type of mesh.
- ∇∇ϕ=const. – no error in the case of squares and hexagons. Triangular meshes and split-quad meshes produce errors.
- ∇∇∇ϕ=const. – all mesh types produce errors. Errors on square meshes are expected to be smaller due to a smaller number of faces contributing to the error.
Laplacian term
The Laplacian term is also approximated as a sum of diffusion fluxes through the faces of the control volume. The analysis is performed by assuming a constant diffusion coefficient, to avoid errors coming from the interpolation of the diffusion coefficient onto the faces. In addition, the surface-normal gradient is modeled using the second-order scheme considering non-orthogonality contributions.
Quadrilateral
A mesh consisting of squares is orthogonal and uniform, and this eliminates a lot of terms in the truncation error for the surface-normal gradient. A stencil of quad cells results in:
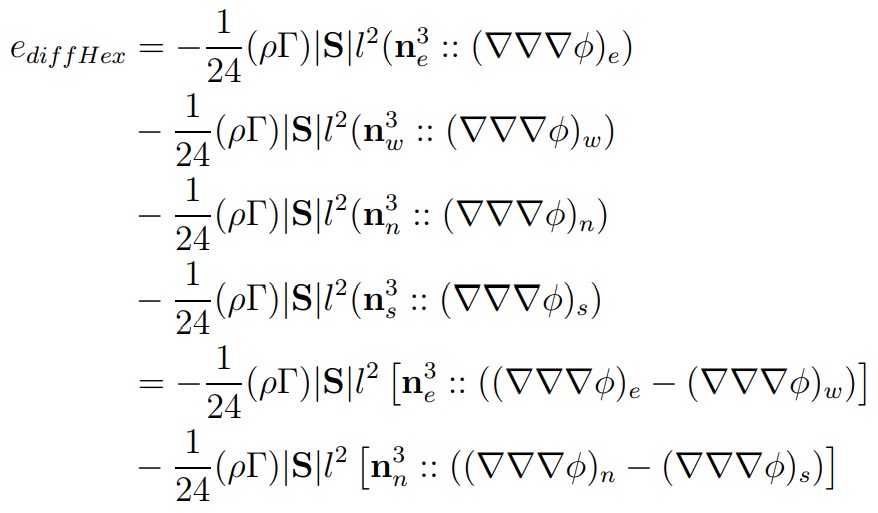
And it shows similar behaviour as for the convection term:
- Errors committed on opposite faces cancel themselves out.
- The approximation is second-order accurate.
Triangle
The mesh consisting of equilateral triangles is both uniform and orthogonal. Summation of truncation errors over faces of a triangle results in:
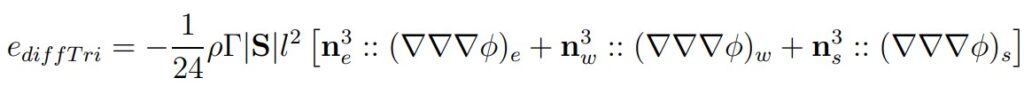
Similarly, it shows:
- Face pairs do not exist; hence the error does not cancel itself out.
- The approximation is second-order accurate.
Hexagon
The mesh consisting of hexagons is also uniform and orthogonal. Summing the errors over the faces of a hexagon results in a truncation error:
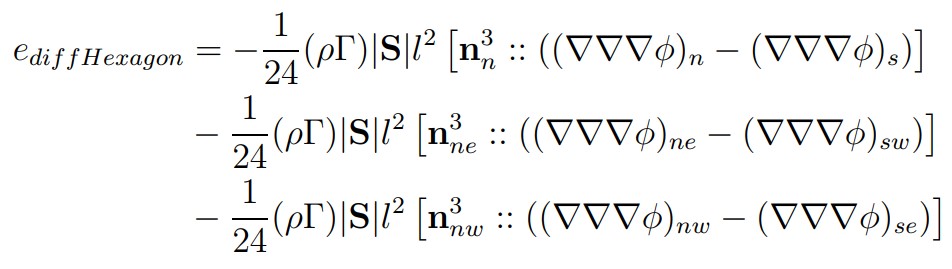
Again, it can be said:
- Errors committed on opposite faces cancel themselves out.
- The approximation is second-order accurate.
Split-square
A mesh consisting of split-square cells is not orthogonal and is still uniform. Summation of errors over the faces of a split hex cell results in:
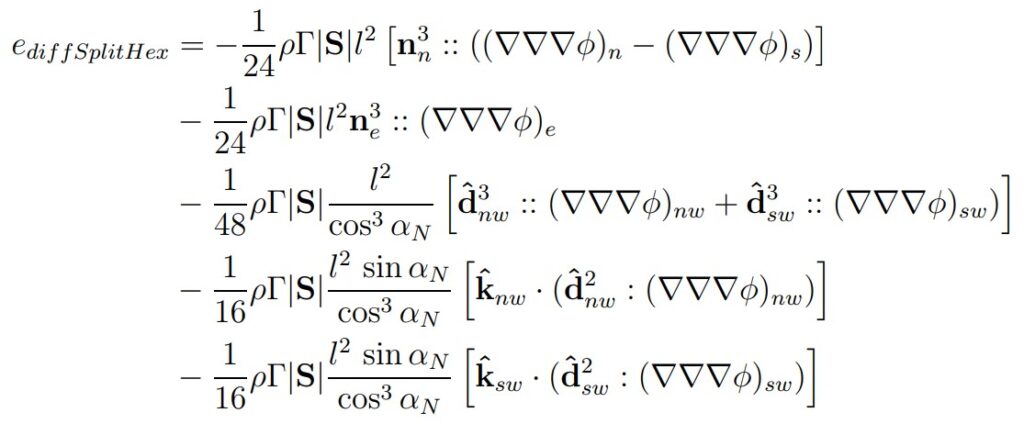
The above equation shows:
- Face pairs do not exist, error cancellation is not as strong as in the case of square meshes.
- The approximation is second-order accurate.
- Non-orthogonality increases the error.
Comparison depending on the solution type
By analyzing the behaviour of the discretisation, depending on the solution type, some interesting conclusions can be drawn:
- ∇∇ϕ=const. – no error on any type of mesh.
- ∇∇∇ϕ=const. – no error in the case of squares and hexagons. Triangular meshes and split-square meshes produce errors.
- ∇∇∇∇ϕ=const. – all mesh types produce errors. Errors on square meshes are expected to be smaller due to a smaller number of faces.
An example
To demonstrate how the analysis above applies in practice let us consider an example of a laminar channel flow over a cavity.
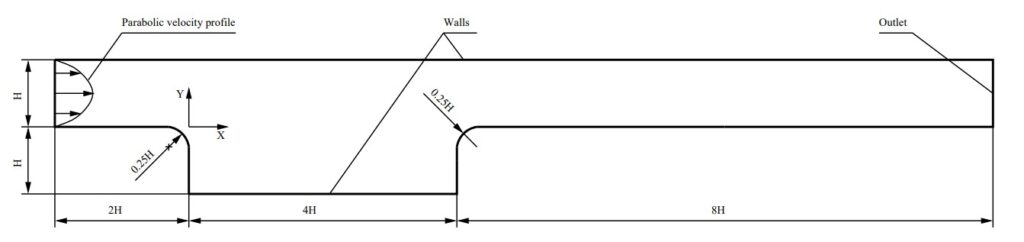
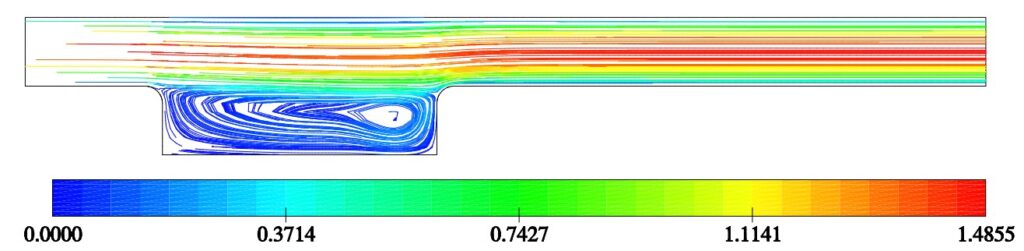
The analysis was performed using three cell types: quadrilaterals, hexagons and triangles.
This flow does not have an analytical solution; hence, a mesh-independent solution was generated by refining the mesh until the changes in the solution dropped below 0.1%. The mesh-independent solution was used to monitor the behaviour of the discretisation error on meshes consisting of various cell types.
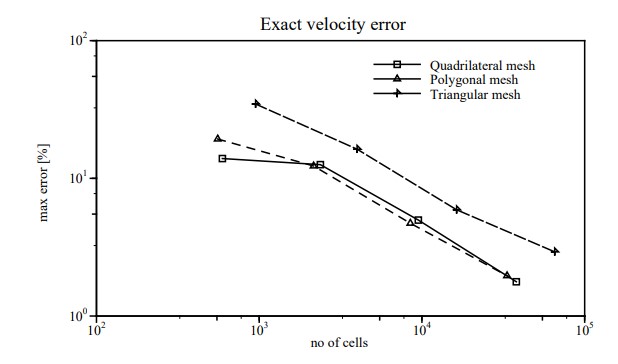
Some conclusions corroborating the theoretical analysis can be drawn here:
- The best accuracy is achieved on a mesh consisting of quad cells.
- Meshes consisting of triangles require an order of magnitude more cells for the same accuracy.
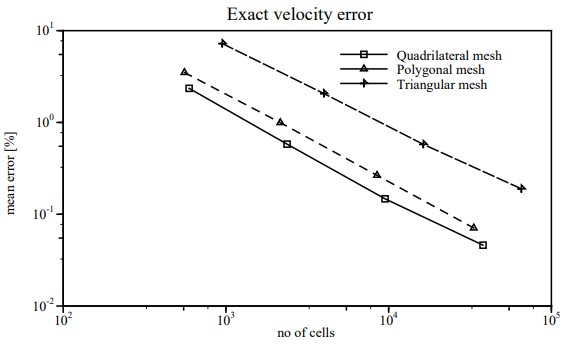
Let us also monitor the pressure drop with mesh refinement. The graph is given below:
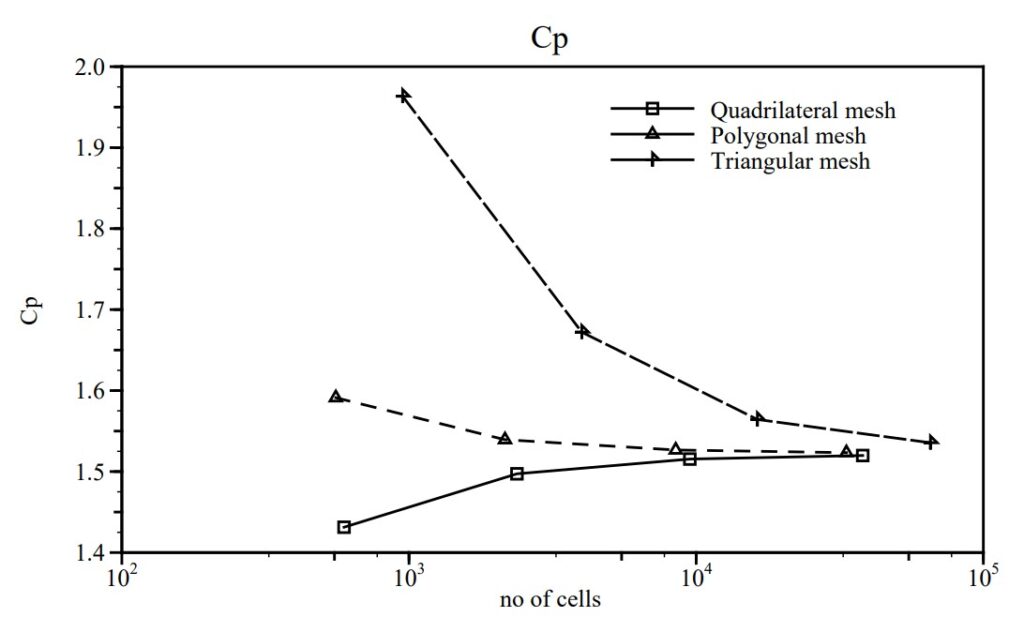
It shows:
- The best accuracy is achieved on a mesh consisting of quad cells.
- Meshes consisting of triangles are diffusive and require an order of magnitude more cells for the same accuracy.
Key takeaways
The most important takeaways about various cell types are:
- Cell types with face pairs shall be preferred because they provide better accuracy for the same number of cells.
- Quadrilateral cells in 2D and hexahedral cells in 3D are the best cell shapes because they have face pairs and have the smallest number of face pairs. However, these meshes are difficult to generate automatically and are often not feasible for extremely complex geometries.
- Meshes consisting of hexagons offer a compromise between accuracy and simplify the process of their automatic generation. However, these meshes require a lot of memory because of many faces and each face usually has five or six vertices.
- Hex-dominant meshes with split-hexes are also a good compromise between accuracy and simplifying the process of mesh generation. They require less memory than the hexagons, which is beneficial if your memory resources are limited. In addition, these meshes performed better than hexagons for cases where the bulk of the flow is aligned with mesh.
- Meshes consisting of triangles and tetrahedra are the least accurate mesh types. However, there are many algorithms for automatic mesh generation, adaptation, etc. and they are used because the process can be automated much easier than for other mesh types. However, they often require an order of magnitude more cells which makes them greedy for computational resources.
Try it yourself
I hope that you have found this post useful and that it has made you curious to try out our latest CF-MESH+, using the knowledge presented in this post, designed to alleviate you from the pain of meshing. You can also subscribe to our newsletter to stay informed on our newest developments.
