Quite often I hear complaints about the required number of non-orthogonality correctors to achieve convergence, and how it’s worthless even trying to run a solver on a mesh, etc.
The point of this series of posts is to give you an overview of the popular myths and to help you understand what’s going on in your Finite-Volume CFD code and how to interpret mesh quality checks for your particular problem. The goal of this post is to de-mystify non-orthogonality and its impact on accuracy.
Non-orthogonality
Non-orthogonality is measured as the angle between the vector connecting neighbouring cell centres at the face and the face-area vector, see the figure below. Low non-orthogonality angles are desired. However, suppose the non-orthogonality increases by about 90 degrees. In that case, the mesh becomes invalid and the discretisation is no longer conservative because the vector connecting cell centres and the face are vector start pointing in opposite directions!
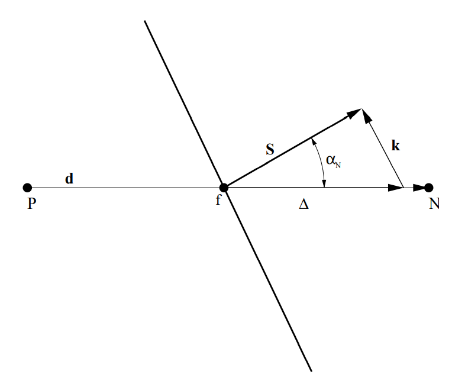
Surface-normal gradient schemes
The scheme for evaluation of surface-normal gradients affects the accuracy of Laplacian terms, and it depends on the non-orthogonality. Convection, divergence, gradient, and source terms are not affected by non-orthogonality. To find out more, see the previous posts.
Most often, the evaluation of the surface-normal gradient is performed as follows:
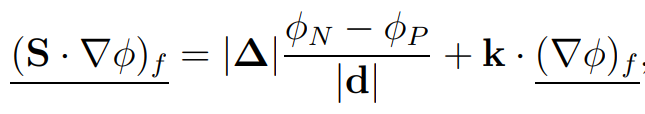
where the first term on the right-hand side is treated implicitly and the second term, representing the non-orthogonality contribution, is treated explicitly as a source term within the solver. This means that it is beneficial to keep non-orthogonality as low as possible to reduce the need to solve equations multiple times until they converge.
Truncation errors
Truncation error for the surface-normal gradient depends on non-orthogonality, and it reads:
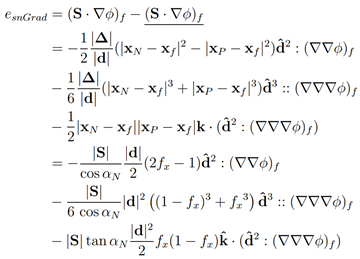
The equation above provides some interesting information:
- The scheme is of first order on non-uniform meshes.
- The error increases significantly with non-orthogonality. It goes to infinity when the angle is 90 degrees because the mesh becomes invalid!
- Non-orthogonality shall be avoided in regions of rapid solution variation. It does not affect accuracy in regions where higher-order gradients are not important.
Laplacian term
Discretisation of the Laplacian terms depends on the interpolation practice for the diffusion coefficient or tensor and the approximation of the surface normal gradient:
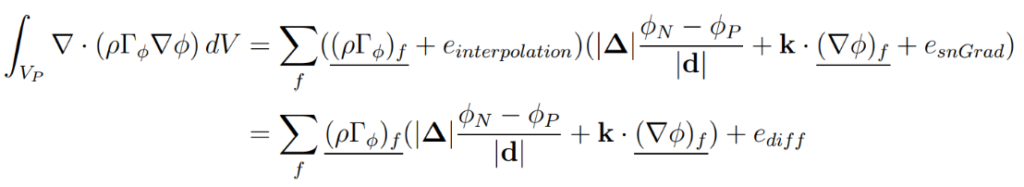
and its truncation error can be written as:
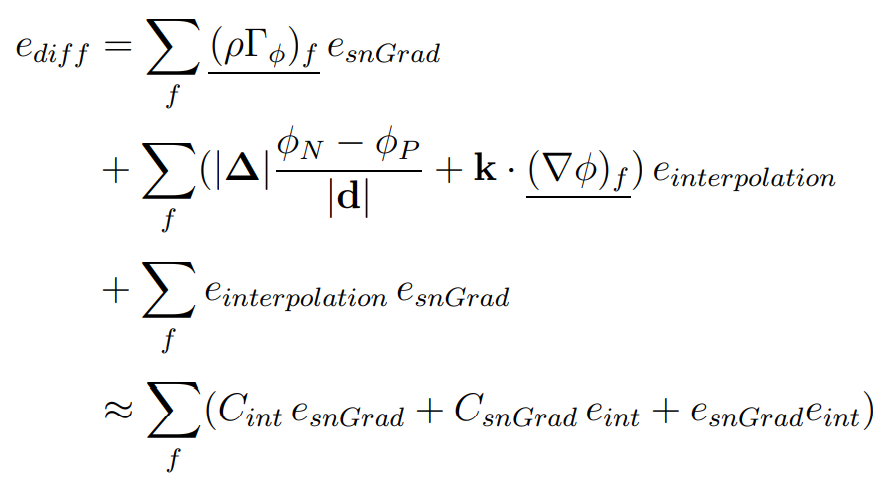
Discretisation error for the Laplacian term is a sum of errors over the faces of a cell, and the total error depends on the number of faces in a cell. The order of the discretisation is dependent on the lowest order scheme used for interpolation or evaluation of surface-normal gradients.
Key takeaways about non-orthogonality
The most important takeaways about non-orthogonality, which I never seem to get tired of telling are:
- It does not affect accuracy in regions where the solution is uniform! Avoid it in jets, boundary layers, and other features where the higher-order gradients are significant.
- It does not affect convection and gradient terms. Hence, it is not the crucial quality measure for convection-dominated flows.
- The influence of non-orthogonality on the calculation of the Laplacian terms, important in the boundary layer region, can be reduced by paying attention to the input geometry used for meshing, as described in Tips & tricks for a high-quality meshing process.
I hope that you have found this post useful and that it has made you curious to try out our latest CF-MESH+, designed to alleviate the pain of meshing. You can also subscribe to our newsletter to stay informed on our newest developments.
