Meshes consisting of arbitrary polyhedra have gained popularity in the CFD community over the last decade, as a consequence of the advances in solver technology. Furthermore, polyhedral meshes can be generated by retrieving the dual of a tetrahedral mesh, and there exist many methods that can generate tetrahedral meshes in complex geometries. In addition, polyhedral meshes have a lower number of cells and better accuracy than their tetrahedral counterpart.
We made an effort to develop an inside-out method for arbitrary polyhedra in cfMesh, for the generation of polyhedral meshes, which does not require high-quality input geometry and is tolerable to small gaps, cracks, and protrusions. Unlike methods that use hex-dominated templates, it is not so sensitive to the alignment of the template with the geometry because most of the mesh faces have either five or six vertices. The method is tested on examples of both academic and industrial interests.
Background and motivation
– Polyhedral meshes provide more accurate solutions than tetrahedral meshes, for the same number of cells
– Significant potential for automation – polyhedral meshes can be generated as a dual of the tetrahedral mesh
– Inside-out methods are proven to be robust and not very sensitive to the quality of the input geometry
– Problems:
1. Complex algorithms are needed to capture concave edges and corners with concave edges
2. Most available tetrahedral meshing tools require high-quality input geometry, which is not always present in the industrial environment
Methodology
The method generates a mesh template from an octree generated using the input surface triangulation with selected feature edges and the user-defined refinement sources. The mandatory refinement source is the maximum cell size in the domain. Other refinement sources are boundary cell size, cell size in local regions of the input surface, and refinement zones that are inside or intersect primitive objects like boxes, spheres, cylinders, and lines.
Furthermore, automatic octree refinement based on curvature estimation and proximity estimation is also available. The octree is refined until the leaves intersecting the surface triangulation and inside the surface are larger than the size specified by the user. The octree is also balanced such that the refinement levels of the leaves attached to a vertex do not differ by more than one. This requirement simplifies the procedure for generation of the initial tetrahedral mesh template which is then converted into a polyhedral template.
User input
– The method requires a surface triangulation enclosing a domain
– Only manifold domains are supported
– Dictionary with user-defined settings, and syntax from OpenFOAM
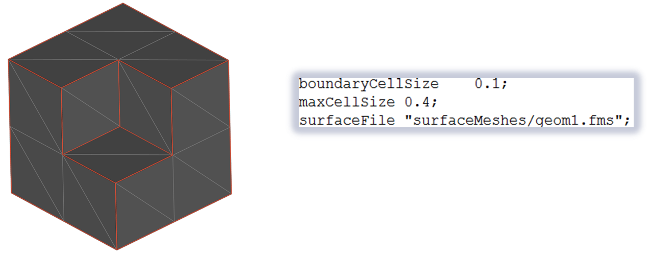
Tetrahedral template
– Generated from a background octree, refined to the users’ criteria
– Based on the BCC arrangement
– Three types of space-filling tetrahedra identified

Polyhedral template
– Generated as a dual of the tetrahedral template
– Cells at the boundary often have many faces not suitable for inside-out methods

Surface preparation/morphing
– Modifies cells at the boundary to have a single boundary face
– Boundary faces are merged into a single face
– Drawback: Some faces deviate from planarity

Capturing of features
– Each boundary face is assigned a region at the input surface where it shall be projected
– Topological correctness is ensured by inserting sheets
– Open problems:
1. Handling of corners with a valence greater than three
2. Smoothing procedure at concave edges

Meshing example: Helicopter
– 0.5 million cells
– Meshing time: 2 minutes
– Non-orthogonality: Max 82o Average 7.3o
– Skewness: Max 6.7 Average 0.092

If you have some cfMesh-related questions, feel free to discuss them in our FB group cfMesh.


