Many problems solved with Computational Fluid Dynamics (CFD) are of an anisotropic nature, such as boundary layers and free surfaces, and they require anisotropic computational meshes to solve these problems efficiently. These features impose stringent requirements on mesh quality and the aspect ratio of computational cells, which requires advanced control of the meshing algorithm. The problem gets even more difficult when dealing with arbitrary polyhedra consisting of faces with more than four vertices because they shall remain flat during the meshing process.
Improvements in cfMesh
In order to improve the robustness and quality of the mesh in the boundary layer, we implemented a novel boundary layer smoother in cfMesh. It improves the orthogonality and the thickness variation of the existing boundary layer, and is therefore applicable in case of poor-quality surface data, and whenever it is possible to generate a valid mesh with the base methodology. The method analyses the mesh for the existence of a boundary layer at the boundaries and analyses the connections between the boundary layer cells.
The quality is improved by smoothing the normal vectors such that their deviation is minimized and the quadrilateral faces in the layer become as flat as possible and orthogonal to the boundary. The thickness variation is controlled via curvature and relative deviation of the thickness over a quadrilateral face connecting two hair edges of the layer. The procedure reduces the thickness in regions failing the criteria in an iterative manner and ensures a smooth transition of the layer thickness over the neighboring cells. The tests show that the algorithm significantly improves the layers, and enables generation of meshes for low-Re simulations.
The anisotropic meshing of regions inside the mesh is achieved via affine modifications of the input surface mesh, and generating the isotropic mesh inside the modified surface mesh. The coordinates of mesh points are mapped back into the original space resulting in an anisotropic volume mesh. The procedure is currently controlled via primitive objects, i.e. boxes and planes, which are prescribed in a dictionary read by cfMesh. The suggested procedure is applicable to meshes consisting of arbitrary cell types. It offers significant potential for reducing the number of cells in regions aligned with geometric objects. In addition, you can further enhance the procedure by adding additional types of sources.
Background and motivation
– Many problems solved with Computational Fluid Dynamics are of an anisotropic nature, and this imposes challenges on efficient meshing
– The common problems tackled in the current study are:
1. Boundary layer generation – extremely difficult when many thin layers are required
2. Free surface flows – anisotropic cells are required in the direction normal to the free surface in order to reduce the number of cells
– The solution shall not be limited to a particular type of cells
Boundary layers
– Problems:
1. Reliable meshing of very thin layers with high-aspect-ratio cells
2. Standard smoothers are not capable of creating high-quality meshes consisting of high-aspect-ratio cells
3. Layers shall exit the domain at inlet/outlet boundaries
4. Most tools require high-quality surface meshes to generate valid layers
– Solutions in cfMesh:
1. Generates a valid mesh, including a boundary layer, and improves the orthogonality and smoothness of the cells in the boundary layer
2. Allows generation of many layers
3. Usable even when the input geometry is of poor quality
4. Parallelized using both SMP and MPI
Boundary layers optimization setting
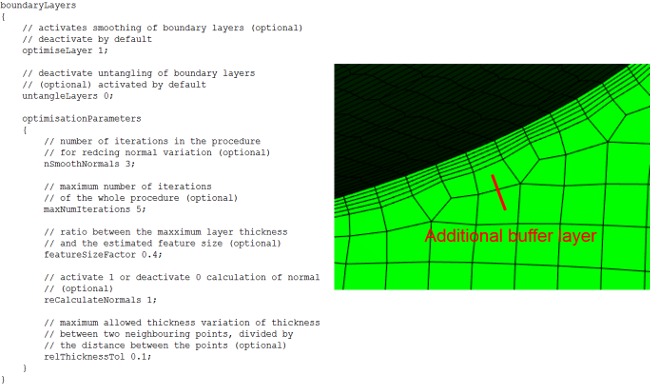
Boundary layers lowRe meshing
– Tested on meshes with up to 50 layers
– Very difficult to achieve without tight control of cell quality
– Sensitive to the smoothness of the mesh’s surface
– Input geometry does not need to be watertight
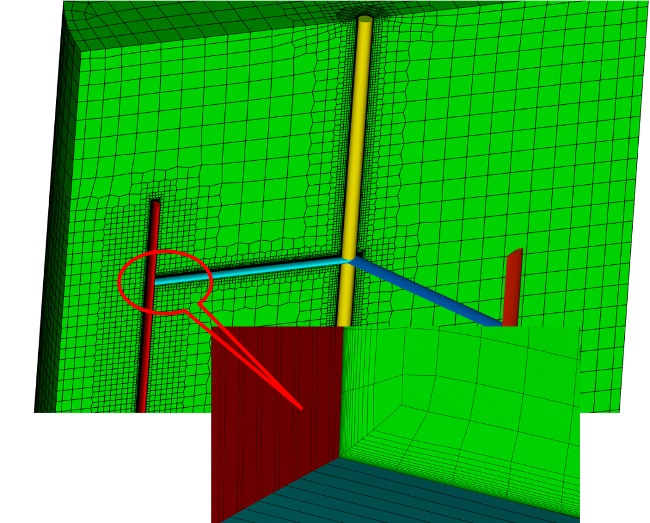
Boundary layers example with dirty geometry
– The procedure is applicable to dirty input data
– Performs best when the input geometry is captured well by the meshing procedure

Boundary layers topology constraints
– Boundary layers extend over concave edges
– Extend over faces connected to corners with a valence greater than three
– Automatically exit at convex boundaries, unless forced otherwise by the above conditions

Anisotropic meshing box scaling
– Linear affine scaling
– Separate scaling factor applicable to every direction
– Applicable to the whole range in each direction

Anisotropic meshing box scaling
– Linear scaling applied to the specified distance from the plane
– Scaling applied in the positive normal direction
– Applied to the whole plane

Meshing examples


If you have any cfMesh-related questions, feel free to join our cfMesh group on Facebook.


